e
Una función lineal según la primera definición dada anteriormente representa una aplicación lineal si y sólo si b = 0. Así, algunos autores llaman función lineal a aquella de la forma f(x) = mx mientras que llaman función afín a la que tiene la forma f(x) = mx + b cuando b es distinto de cero.
Ejemplo:
Una función lineal de una única variable dependiente x suele escribirse en la forma siguiente
que se conoce como ecuacion de la recta en el plano xy.
En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
en esta recta el parámetro m= 1/2, esto es el crecimiento de la recta es 1/2, cuando aumentamos x en una unidad, y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2
La ecuación:
la pendiente de la recta, el parámetro m= -1, indica que cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad, el corte con el eje y, lo tiene eny= 5, dado que el valor de b= 5.
En el caso de una recta el valor de m se corresponde al ángulo de inclinación de la recta con el eje de las x a través de la expresión:

y = mx
Su gráfica es una línea recta que pasa por el origen de coordenadas.

y = 2x
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y = 2x | 0 | 2 | 4 | 6 | 8 |

Pendiente
m es la pendiente de la recta.
Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.


La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Si m < 0 la función es decreciente y el ángulo que forma
la recta con la parte positiva del eje OX es obtuso.
la recta con la parte positiva del eje OX es obtuso.






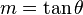

0 comentarios:
Publicar un comentario