En mecánica clásica, el trabajo que realiza una fuerza se define como el producto de ésta por el camino que recorre su punto de aplicación y por el coseno del ángulo que forman el uno con el otro. El trabajo es una magnitud física escalar que se representa con la letra 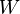 (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
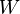 (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.
(del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.Matemáticamente se expresa como:
Donde 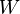 es el trabajo mecánico,
es el trabajo mecánico, 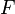 es la magnitud de la fuerza,
es la magnitud de la fuerza,  es el desplazamiento y
es el desplazamiento y  es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).
es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).
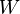 es el trabajo mecánico,
es el trabajo mecánico, 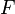 es la magnitud de la fuerza,
es la magnitud de la fuerza,  es el desplazamiento y
es el desplazamiento y  es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).
es el ángulo que forman entre sí el vector fuerza y el vector desplazamiento (véase dibujo).Cuando el vector fuerza es perpendicular al vector desplazamiento del cuerpo sobre el que se aplica, dicha fuerza no realiza trabajo alguno. Asimismo, si no hay desplazamiento, el trabajo también será nulo.
El trabajo en la Mecánica:
Consideremos una partícula P sobre la que actúa una fuerza F, función de la posición de la partícula en el espacio, esto es F = F(r), y sea dr un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo dt. Llamamos trabajo elemental, dW, de la fuerza F durante el desplazamiento elemental dr al producto escalar de F por dr; esto es,

Si representamos por ds la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es ds = |dr| , entonces el vector tangente a la trayectoria viene dado por et = dr/ds y podemos escribir la expresión anterior en la forma

donde θ representa el ángulo determinado por los vectores F y et y Fs es la componente de la fuerza F en la dirección del desplazamiento elemental dr.
El trabajo realizado por la fuerza F durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo θ sea agudo, recto u obtuso.
Si la partícula P recorre una cierta trayectoria en el espacio, su desplazamiento total entre dos posiciones A y B puede considerarse como el resultado de sumar infinitos desplazamientos elementales dr y el trabajo total realizado por la fuerza F en ese desplazamiento será la suma de todos esos trabajos elementales; o sea

Esto es, el trabajo viene dado por la integral curvilínea de F a lo largo de la curva C que une los dos puntos; en otras palabras, por la circulación de F sobre la curva C entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza F sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.
En el caso particular de que la fuerza aplicada a la partícula sea constante (en módulo, dirección y sentido), se tiene que
o sea que el trabajo realizado por una fuerza constante viene expresado por el producto escalar de la fuerza por el vector desplazamiento total entre la posición inicial y la final.
Si sobre una partícula actúan varias fuerzas y queremos calcular el trabajo total realizado sobre esta ella, entoncesrepresentará al vector resultante de todas las fuerzas aplicadas.






0 comentarios:
Publicar un comentario